Dziś wpis edukacyjno rozrywkowy o ciągu Fibonacciego i złotej proporcji w przyrodzie. Tak zwany ciąg Fibonacciego odkrył matematyk Leonardo z Pizzy w 1202 roku. Zwany Fibonaccim, gdyż taki zyskał przydomek po ojcu (syn Bonaccia). Opisał go w dziele Księga rachunków (Liber abbaci). Pomogły mu w tym króliki. Obserwował, jak rozwija i powiększa się jego stadko. Jako matematyk założył, że jeśli ma parkę młodych królików (samca i samicę) w pierwszym miesiącu to one dorastają w kolejnym miesiącu i już w trzecim miesiącu są w stanie wydać potomstwo - załóżmy, że znów parę (samca i samicę). Tworzy nam się model matematyczny. Każda młoda para jest w stanie po 2 miesiącach od narodzin począć nową parę, a dorosła para królików rozmnaża się potem co miesiąc. Po kilku miesiącach mamy już niezłe stadko.
Liczby par królików w ciągu Fibonacciego
Początkowo mamy 1 parę. Po miesiącu nadal 1 parę - już dojrzałą. Po 2 miesiącach są już 2 pary - stara i młoda. Po 3 miesiącach stara ma kolejną młodą, pierwsza młoda para dojrzewa. Zatem mamy 3 pary. Policzmy jeszcze jeden miesiąc dalej. Stara para ma już kolejną parę. Pierwsza młoda para już ma potomstwo. Doszły zatem 2 pary więc w sumie mamy 5 par. I tak dalej, i tak dalej... W tym miejscu przerywam metodę opisową a przedstawię metodę dużo prostszą - obliczeniową. Otóż okazuje się, że w każdym kolejnym miesiącu liczba par królików równa jest sumie liczb par królików z dwóch poprzednich miesięcy. Tak powstaje właśnie słynny ciąg Fibonacciego. Zobaczcie:
1
1
2 = 1+1
3 = 2+1
5 = 3+2
8 = 5+3
13 = 8+5
21 = 13+8
34 = 21+13
55 = 34+21
89 = 55+34
itd.
W sumie wystarczy zapamiętać początek ciągu, a kolejne wartości bardzo łatwo wyliczyć. Niestety nie ma wzoru na wyliczenie dokładnie n-tego wyrazu Fn za pomocą liczb całkowitych. Są nieco skomplikowane wzory, których tu nie będę teraz przytaczał, ale do nich wrócę później.
Ciąg Fibonacciego w świecie roślin
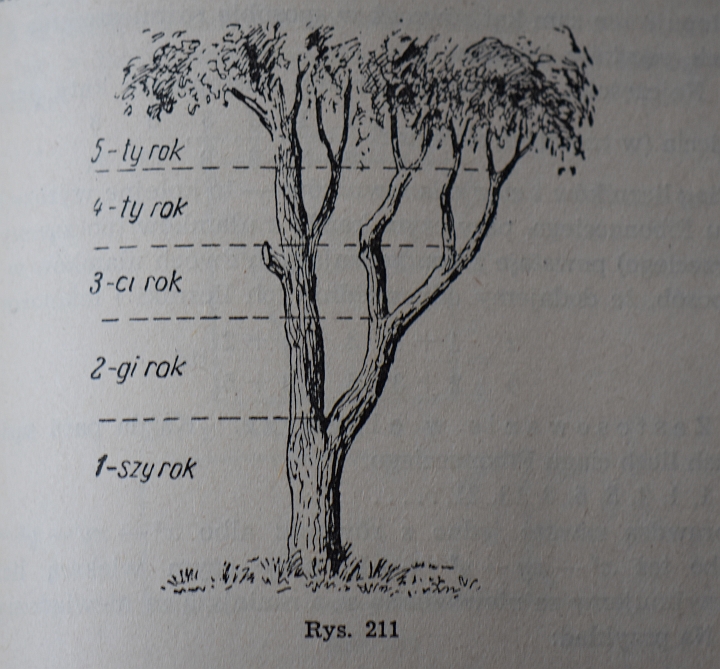
Ilustracja z B. Kordiemski "Rozrywki matematyczne"
Pewnie pamiętacie, jak główny bohater w "Kodzie Leonarda da Vinci" rozwiązuje zagadkę związaną z tym ciągiem? Ale książka czy film to jedno, a życie to drugie. Liczby z ciągu Fibonacciego pojawiają się często w przyrodzie. Liczby płatków kwiatów zazwyczaj są liczbami z tego ciągu. Trójlist, bez - 3 płatki, fiołek, jaskry - 5 płatków, ostróżka 8, aksamitka, nagietek 13, cykoria, aster 21, stokrotka, złocień 34, a słonecznik albo 55, 89 albo nawet 144 płatki. Róże kalafiora też układają się spiralnie i liczba spiral to liczba z tego ciągu. A jeśli widzimy liczbę płatków inną niż liczba z tego ciągu? Zawsze matematyk może to wytłumaczyć, że jakiś płatek się urwał czy został zerwany :-) A biolog powie, że świat nie jest taki idealny, jak w matematycznych modelach.
Przejdźmy teraz do owoców - banan w przekroju ma 3 części, jabłko ma pięcioramienną gwiazdę utworzoną z gniazd nasiennych, persymona natomiast 8. Ciekawie jest u ananasa - jego powierzchnia jest pokryta segmentami, które splecione tworzą 2 rodziny spiral. Jedna okręca się wokół ananasa w przeciwnym kierunku do ruchu wskazówek zegara i zawiera 8 spiral. Druga zgodna z ruchem wskazówek ma 13 spiral. Liczby z ciągu spotkamy też w szyszkach sosen - wystarczy policzyć liczby łusek w spiralach. Skomplikowane wzory można też spotkać w układzie ziaren słonecznika. Zachęcam do lektury specjalistycznych artykułów na ten temat.
Wrócę na moment do szyszek. W 1968 roku Alfred Brosseau, matematyk z USA, przebadał 4290 szyszek z 10 różnych gatunków sosny pinii z Kalifornii. Okazało się, że 98,3% próbek sosen reprezentowało liczby z ciągu Fibonacciego. Świat nauki nie uwierzył w wyniki badania. W 1992 roku powtórzył je botanik Roger Jean z Kanady. Przebadał 12 750 próbek z 650 różnych gatunków i otrzymał wynik na poziomie 92%. Dacie wiarę?
Możemy teraz rozważyć jeszcze rozwój muszli ślimaka. Tu też zauważymy liczby z ciągu Fibonacciego. Muszla przyrasta bazując na rozmiarze dwóch poprzednich przyrostów. Powstaje spirala. Dzieło wręcz idealne.
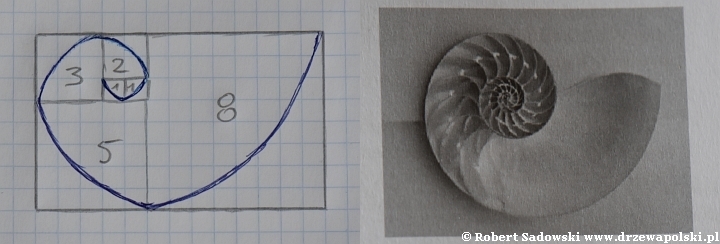
A jak to wygląda z roślinami i drzewami?
Taki ciąg występuje, gdy opisujemy liczbę nowo powstałych pędów rośliny wyrastających w jednym sezonie wegetacyjnym. Zjawisko zwane spiralną filotaksją (ulistnienie Fibonacciego) cechuje wiele gatunków drzew i roślin. Na czym to polega? Chodzi o strukturę gałęzi, które układają się wokół pnia. A u roślin chodzi o rozłożenie liści. Ich rozkład i liczby nie są losowe. One rosną tak, aby mieć jak największy dostęp do słonecznego światła i spływającego do korzeni deszczu. Żeby zasłaniać, jak najmniejszą liczbę (powierzchnię) pozostałych, niżej położonych liści, a w ogóle nie zasłaniać swoich sąsiadów. Walka jest też o optymalne wykorzystanie posiadanej przestrzeni wokół drzewa czy rośliny.
Oczywiście chodzi tu o model matematyczny i rozważania teoretyczne. Jeśli by tak założyć, to licząc gałęzie na odpowiednich wysokościach łatwo byłoby policzyć wiek drzewa. Tak idealnie najczęściej jednak nie jest.
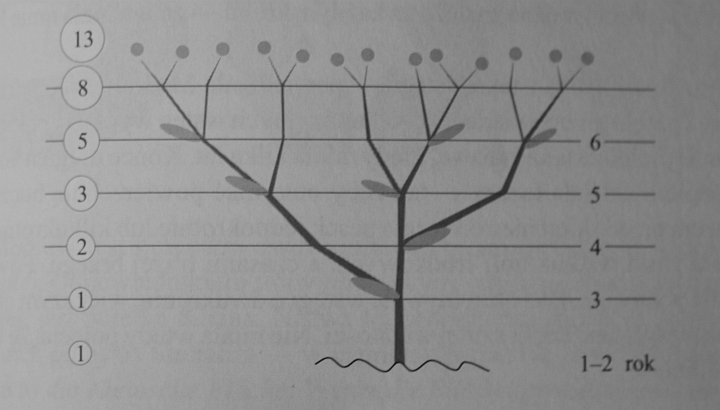
Ilustracja z "Odlotowa matematyka" część 2, Zdzisława Głowackiego.
Jak roślina wypuszcza nowe liście to każdy następny znajduje się powyżej tego już wypuszczonego i jest przesunięty w bok. Dla każdego gatunku roślin można określi ten kąt przesunięcia liści. Z grubsza jest on zachowany dla całej danej rośliny. Kąt ten podawany jest jako ułamek, który wyraża część całego okręgu. Ten sam kąt dotyczy się nie tylko liści ale również pączków i kwiatów.
Co ciekawe najczęściej spotykane kąty przesunięcia to 1/2, 1/3, 2/5, 3/8, 5/13, 8/21... Wygląda znajomo? Liczniki i mianowniki są liczbami Fibonacciego! Ale to nie wszystko. Każdy kolejny kąt powstaje, jeśli dodamy dwa poprzednie ale w sprytny sposób. Licznik do licznika, a mianownik do mianownika.
Złota proporcja
Liczby Fibonacciego są blisko związane ze złotą proporcją i liczbą φ. Złotą proporcję najłatwiej pojąć, gdy mamy prostokąt i musimy go tak podzielić na dwie części aby znaleźć inny prostokąt o tych samych proporcjach boków. Tniemy na kwadrat i mniejszy prostokąt i zachowujemy proporcję boków. Przykład (z Wikipedii):
Ten mały, różowawy prostokąt jest tak samo "kształtny", jak duży prostokąt.
Czyli (a+b)/a = a/b, co daje φ = (1+√5)/2, co w przybliżeniu równa się 1,618034.
Inaczej można zaprezentować jeszcze złotą proporcję przy podziale odcinka. Mamy dowolny odcinek i trzeba go podzielić na 2 części, tak by stosunek dłuższej części do krótszej był taki sam, jak stosunek całego odcinka do dłuższej części. Rozwiązaniem jest liczba φ.
Z ciekawostek warto podać, że φ = 1+1/φ.
A jaki jest związek złotej proporcji z ciągiem Fibonacciego? Okazuje się, że iloraz kolejnych dwóch sąsiadujących liczb Fibonacciego zbliża się do złotej liczby φ :-). Podzielcie sobie większą przez mniejszą i już przy dziesiątym ilorazie uzyskacie bardzo dobre przybliżenie. Co więcej, możemy już wrócić do podania wzoru na n-tą liczbę Fibonacciego.
Fn = [φn - (-φ-n)]/√5
Wygląda skomplikowanie, ale warto wiedzieć, że jest taki związek.
I na koniec złota proporcja i świat drzew. Oto przepiękny przykład proporcjonalności liści wiązu górskiego i figowca pospolitego:
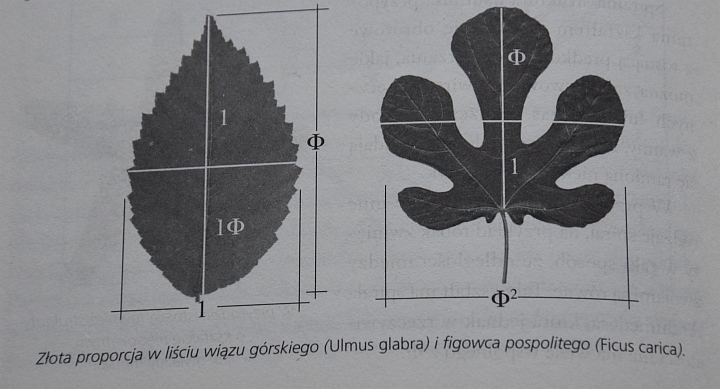
Ilustracja z książki Fernando Corbalan "Złota Proporcja"
Oczywiście temat jest dużo szerszy. Zarówno złota proporcja, jak i ciąg Fibonacciego, mają zastosowanie w sztuce, architekturze, muzyce,... Jest wiele ciekawostek wynikających z tych liczb. Ale to już wchodzenie w nieco głębszą matematykę.
Dużo ciekawych przykładów na liczby Fibonacciego w przyrodzie znaleźć można na stronie: https://www.projektpulsar.pl/srodowisko/2097379,1,rosliny-licza.read
Brak komentarzy:
Prześlij komentarz